Z=log k to base 6 and upon further simplification we get Thus 1/z will be equal to log 6 to base k Now upon adding 1/x1/y1/z will be equal to log 2 to base k log 3 to base k log 6 to base k Which will Continue Reading Given 2^x=3^y=6^z Lets assume that each and every term is equal to k Which implies Without actual division, show that (x – 1)^2n – x^2n 2x – 1 is divisible by 2x^3 – 3x^2 x asked in Polynomials by Harithik ( 243k points) polynomialsThere are infinite solutions as you have 3 variables but only one equation However, it is interesting to note that there is no solution for which all of the varibles x,y,z are integersFermat's last theorem says that there is no solution of x^n

How To Prove Xyz 1 3 Le X Y Z 3 Using Linear Algebra Mathematics Stack Exchange
3^x=4^y=12^-z find 3/x+3/y+3/z
3^x=4^y=12^-z find 3/x+3/y+3/z-EULERS LINKS solve z homogeneous function degree n show x^2Ә^2u/Әx^2 y^2Ә^2u/Әy^22xy^2u/Әx Әy =n(n1)z https//youtube/gnn51DwOhA If u=x/(yz)y/(xz)(xyz)^3 put xy = a (az)^3= a^3 z^3 3az ( az) = (xy)^3 z^3 3 a^2 z 3a z^2 = x^3y^3 z^3 3 x^2 y 3 x y^2 3(xy)^2 z 3(xy) z^2 =x^3 y^3 z^3 3 x




X 3 Y 3 Z 3 Xyz Novocom Top
Factorize x^3 y^3 z^3 = 3xyzFactor (x^3y^3z^3 ) WolframAlpha Rocket science?Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more
Not a problem Unlock StepbyStepRewrite the expression x y z = 3 ⋅ a x y z = 3 ⋅ a xy z = 3a x y z = 3 a Move all terms not containing y y to the right side of the equation Tap for more steps Subtract x x from both sides of the equation y z = 3 a − x y z = 3 a x Subtract z z from both sides of the equation y = 3 a − x − z y = 3 a x zUnlock StepbyStep x^3 y^3 z^3 = 42 Extended Keyboard Examples Download Page POWERED BY THE WOLFRAM LANGUAGE
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more X, y, z যদি তিনটি স্বতন্ত্র ইভেন্ট হয় তবে তা প্রমাণ করুন 11k (xy)^3 (yz)3 (zx)^3 = 3(xy)(yz)(zx) That is it no constraints etc It mentions "This can be done by expanding out the brackets, but there is a more elegant solution" Homework Equations The Attempt at a Solution First of all this only seems to hold in special cases as I have substituted random values for x,y and z and they do not agree




Linear Algebra Would Like A Hint On How To Show Xyz X Y Z 3 Learnmath




If X Y Z 0 Show That X 3 Y 3 Z 3 3x Y Z
I don't know what you really want to ask , but here is at least a bit of content to this for this formula Since it is homogenous in x,y,z (so all terms have equal degree), you can read it as a description of a object of algebraic geometry eitherNote that, by the Arithmetic MeanGeometric Mean Inequality 3 = x y z = x 3 y 3 z 3 ≥ 3 x 3 y 3 z 3 3 = 3 x y z, so that x y z ≤ 1 Since x, y, and z are (assumed to be positive) integers, the only solution that works is x = y = z = 1 Share edited Oct 11(xyz)^3 (x y z) (x y z) (x y z) We multiply using the FOIL Method x * x = x^2 x * y = xy x * z = xz y * x = xy



X Y Z 2 X2 Y2 22 3 X Y Z 4 X3 Y3 Z3 Gauthmath




Express X 3 Y 3 Z 3 3x Y Z X 2 Y 2 Z 2 X Y Y Z Zx In Low
Use sum of cubes identity to find x^3y^3z^3 = (xyz)(x^2y^2xyzz^2) Use the sum of cubes identity a^3b^3=(ab)(a^2abb^2) with a=xy and b=z as follows x^3y^3z^3 =(xy)^3z^3 =((xy)z)((xy)^2(xy)zz^2) =(xyz)(x^2y^2xyzz^2)Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreSimplifying X 3 y 3 = z 4 Solving X 3 y 3 = z 4 Solving for variable 'X' Move all terms containing X to the left, all other terms to the right Add '1y 3 ' to each side of the equation X 3 y 3 1y 3 = 1y 3 z 4 Combine like terms




X Y Z 0 Show That X3 Y3 Z3 3xyz Novocom Top
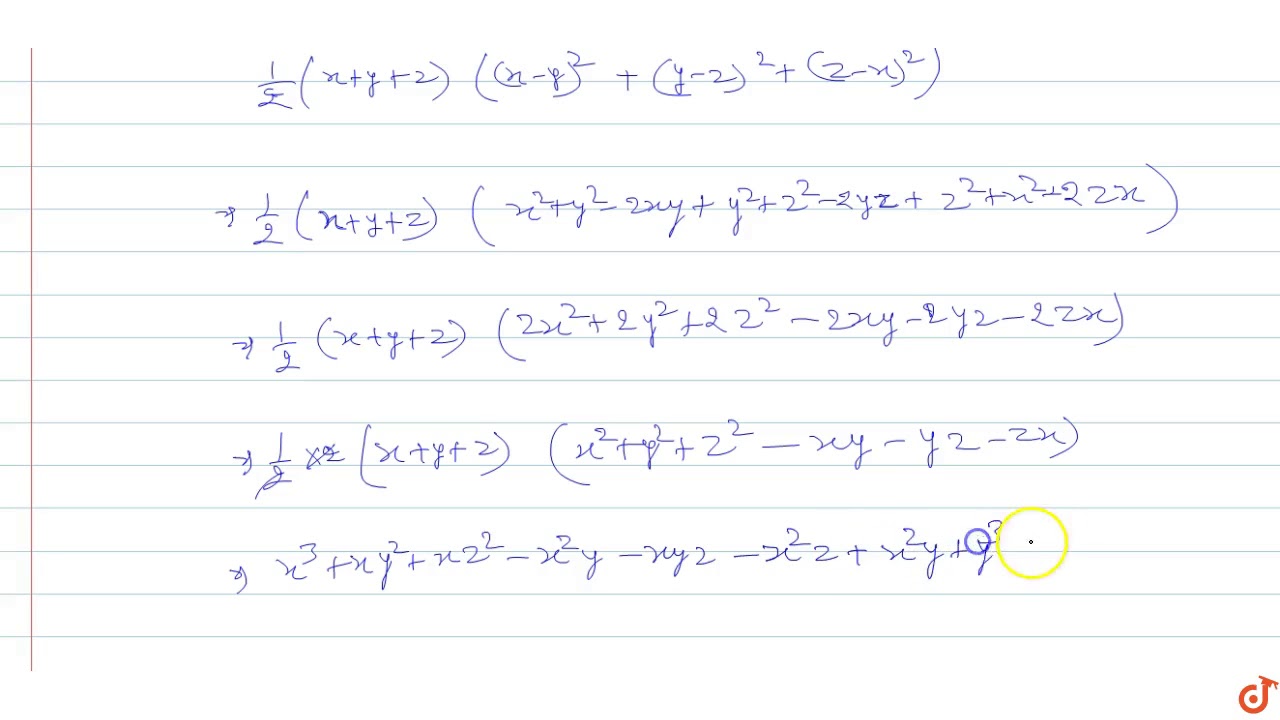



Verify That X 3 Y 3 Z 3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW 2x 3 y 3z =5 , x 2y z=4 , 3x y2z = 3Click here👆to get an answer to your question ️ Verify that x^3 y^3 z^3 3xyz = 1/2(x y z)(x y)^2 (y z) (z x)^2Equations Tiger Algebra gives you not only the answers, but also the complete step by step method for solving your equations x3(yz)y3(zx)z3(xy) so that you understand better
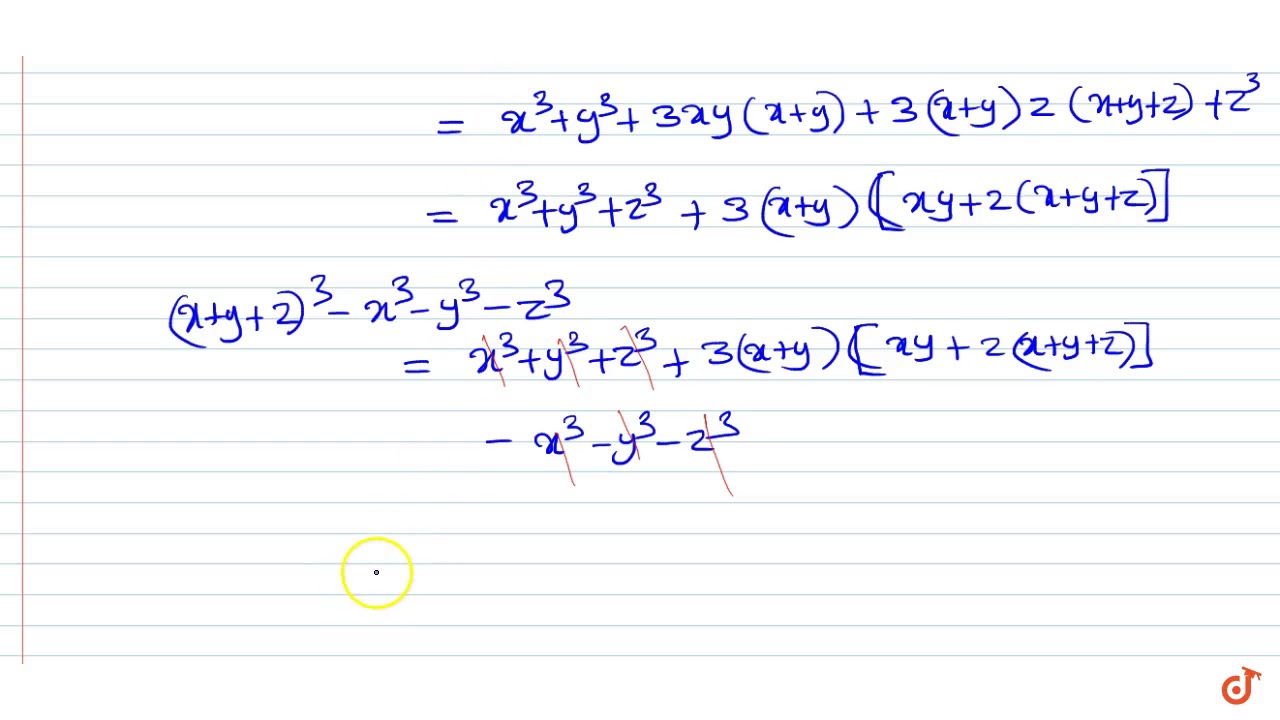



Factorise The Expression X Y Z 3 X 3 Y 3 Z 3 Into Linear Factors Youtube



Solved Solve The System X Y Z 3 2x Y 3 Select One Y 2x 3 6 3x B X 2x 3 6 3x C Z 2x 3 6 3x D No Solution E Course Hero
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreY=xz/3 Simple and best practice solution for y=xz/3 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more




How To Prove Xyz 1 3 Le X Y Z 3 Using Linear Algebra Mathematics Stack Exchange




Solution Simplify X 2 Y 3 Z 2 3 X 3 Yz 3 1 2 Xyz 3 5 2
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Verify that `x^3y^3z^33x y z=1/2(xyz)(xy)^2(yz)^2(zx)^2`Solve by Substitution 2xyz=3 , 3xy3z=3 , x3y2z=3, , Move all terms not containing to the right side of the equation Tap for more steps Subtract from both sides of the equation Add to both sides of the equation Replace all occurrences of with in each equation Tap for more stepsSimple and best practice solution for xyz=3 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so



If Math X Y Z 0 Math How Do You Prove That Math X 3 Y 3 Z 3 3xyz Math Quora
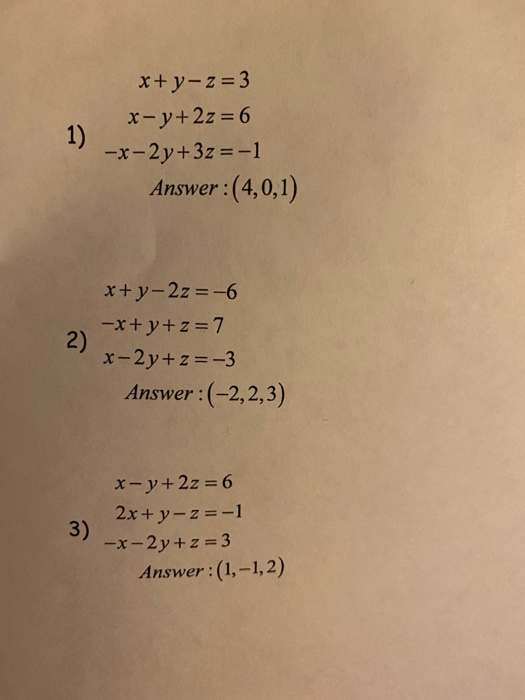



1 X Y Z 3 X Y 2z 6 X 2y 3z 1 Answer 4 0 1 Chegg Com
1 = 1 3 ( x 3 y 3 z 3) ≤ 1 3 ( x y z) 3 = 1 Equality only holds when x = y = z = 1 Let's replace z ↦ − z and try to solve the system of equations for x, y, z ≥ 0 x 3 y 3 = 3 z 3 and x y = z 3 We can still use the power mean inequality (inStep 1 Equation at the end of step 1 ((3 • (x y z) x3) y3) z3 Step 2 Trying to factor by pulling out 21 Factoring x33xy33yz33z Thoughtfully split the expression at hand into groups, each group having two terms Group 1 y33y Group 2 x33x We know that x3 y3 z3 3xyz = (x y z) (x2 y2 z2 xy yz zx) Putting x y z = 0, x3 y3 z3 3xyz = (0) (x2 y2 z2 xy yz zx) x3 y3 z3 3xyz = 0 x3 y3 z3 = 3xyz Hence proved Show More Ex 25 Ex 25, 1 Ex 25,2 Important Ex 25,3 Important Ex 25,4
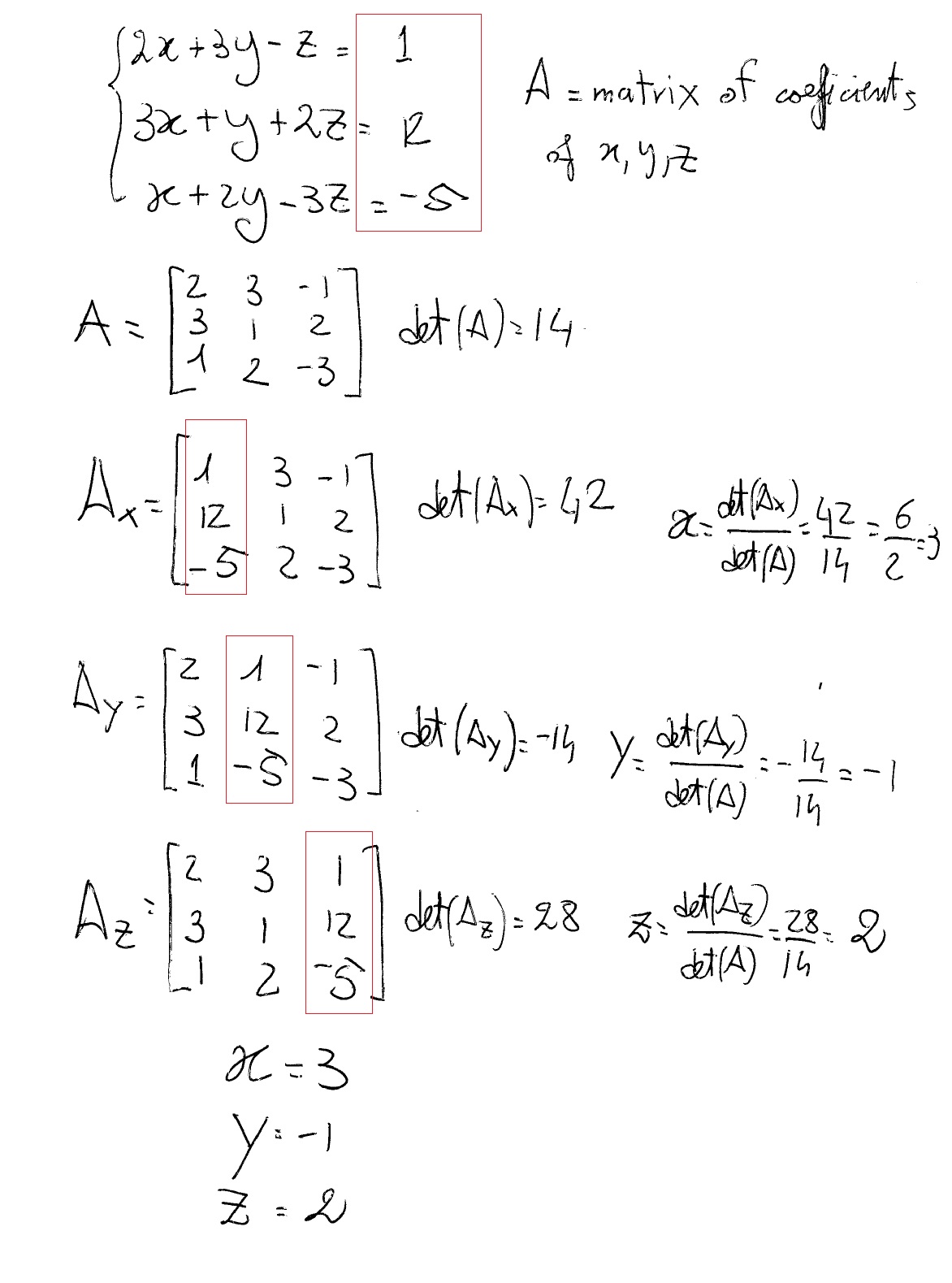



How Do You Solve 2x 3y Z 1 3x Y 2z 12 And X 2y 3z 5 Socratic




2 Two Cube 5 Five Cube 10 Ten Cube Pdf Free Download
The proof that follows is based on the infinite descent, ie, we shall show that if $(x,y,z)$ is a solution, then there exists another triplet $(k,l,m)$ of smaller integers, which is also a solution, and this leads apparently to a contradiction(1) "z3" was replaced by "z^3" 2 more similar replacement(s) Step 1 Trying to factor as a Sum of Cubes 11 Factoring x 3 y 3 z 3 Theory A sum of two perfect cubes, a 3 b 3 can be factored into (ab) • (a 2abb 2) Proof (ab) • (a 2abb 2) = a 3a 2 b ab 2 ba 2b 2 a b 3 = a 3 (a 2 bba 2)(ab 2b 2 a) b 3 = a 3 Chứng minh rằng ( x y z ) 3 x 3 y 3 z 3 = 3 ( x y ) ( y z ) ( z x ) Theo dõi Vi phạm YOMEDIA Toán 8 Bài 9 Trắc nghiệm Toán 8 Bài 9 Giải bài tập Toán 8 Bài 9




If X Y Z 9 And Xy Yz Zx 23 The Value Of X 3 Y 3 Z 3 3xyz Edurev Class 9 Question




A If X 3 Y 3 Z 3 3 X Y Z And X Y Z 0 Find Frac X Y 2 X Y Frac Y Z 2 Y Z Frac Z X 2 Z X
These are the possible solution (values for x and y and z) Thus, getting x^5y^5z^5 will get us a value of Image transcriptions 3 Equation System Solver X Egn 1 xtyz=3 Egn 2 x*3ty33= Egn 3 x 4ty~4z*4= Submit (x y z = 3, x'y' 2' = 15, x y 2* = 35 Real solutions Approximate forms More solutions x =1, y=1 v2 , z=1v2 x =1, y=1v2 , z=1v2 x=1 V2, y=1, z=1v2 x=1 V2 , yEvaluate an expression 41 Multiply (zx)3 by (zx) The rule says To multiply exponential expressions which have the same base, add up their exponents In our case, the common base is (zx) and the exponents are 3 and 1 , as (zx) is the same number as (zx)1 The product is therefore, (zx)(31) = (zx)4 The answer is yes, the rational points on your surface lie dense in the real topology Let's consider the projective surface S over Q given by X 3 Y 3 Z 3 − 3 X Y Z − W 3 = 0 It contains your surface as an open subset, so to answer your question we might as well show that S ( Q) is dense in S ( R) Observe that S has a singular




New Question Verify That X3 Y3 Z3 3xyx 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Tex Textless H2 Brainly In




X 3 Y 3 Z 3 क म न ज ञ त क ज ए यद X Y Z 15 Xy
Solution for Z=3xy equation Simplifying Z = 3x 1y Solving Z = 3x 1y Solving for variable 'Z' Move all terms containing Z to the left, all other terms to the right Simplifying Z = 3x 1y View Full Answer Deep Sah, added an answer, on 3/10/15 Deep Sah answered this We know that a^3 b^3 c^3 3abc = (a b c) (a^2 b^2 c^2 ab bc ac) Take, a = xy, b = yz, c = zx we get, (xy)^3 (yz)^3 (zx)^3 3 (xy) (yz) (zx)To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Factorise the expression `(xyz)^3x^3y^3z^3` into linear factors




Solve The Following System Of Linear Equations By Matrix Method X Y Z 3 2x Y Z 2 X 2y 3z 2 Youtube



1
On x^3 x y^3 y = z^3 z Suppose we wish to find an infinite set of solutions of the equation x^3 x y^3 y = z^3 z (1) where x, y, z are integers greater than 1 If z and x are both odd or both even, we can define integers u and v such that z=uv and x=uvAnswer by lenny460 (1073) ( Show Source ) You can put this solution on YOUR website! Show that $$(xy)^3(yz)^3(zx)^3 = 3(xy)(yz)(zx)$$ This can be shown through expansion but there is a more elegant solution I cannot discover anything I would consider elegant Can anyone h



Using Properties Of Determinants Prove That X Y Z X 2 Y 2 Z 2 X 3 Y 3 Z 3 Xyz X Y Y Z Z X Sarthaks Econnect Largest Online Education Community




X 3 Y 3 Z 3 Xyz Novocom Top
Click here👆to get an answer to your question ️ Factorise the expression , (x y z )^3 x^3 y^3 z^3 into linear factors



What Will Be The Value Of X Y Z 3 If X Y Z 0 Quora




Solve The Following System Of Equations By Crout S Method X Y Z 3 2x Y 3z 16 And 3x Y Z 3 Mathematics 3 Question Answer Collection




If X Y Z 0 Show That X3 Y3 Z3 3 Xyz Brainly In




Prove That Det X X 2 X 3 Y Y 2 Y 3 Z Z 2 Z 3 Xyz X Y Y Z Z X Youtube
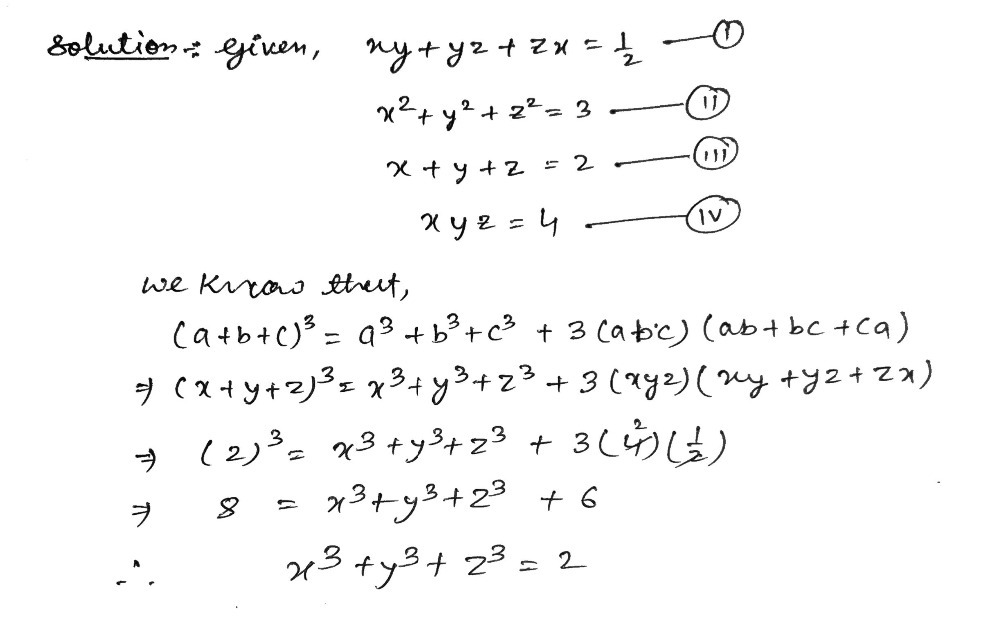



X Y Z Z X 1 2 X2 Y2 Z2 3 X Y Z 2 X Y Z 4 Gauthmath




If X Y Z 1 Xy Yz Zx 1 And Xyz 1 Find The Value Of X3 Y3 Z3 Maths Polynomials Meritnation Com




If X 1 3 Y 1 3 Y 1 3 0 Then X Y Z 3 27x Y Z Youtube



Services Artofproblemsolving Com Download Php Id Yxr0ywnobwvudhmvzs8xl2u2m2vizddlyjk1zgm4m2ixmdqzotc2zdq5ndhmmdy3m2fiztfk Rn Vxnlznvsiefsz2vicmfpyybnyw5pchvsyxrpb25zlnbkzg




Q If X Y Z 1 Xy Yz Zx 1 And Xyz 1 Find The Value Of X3 Y3 Z3 Maths Polynomials Meritnation Com




Ex 2 5 12 Verify That X3 Y3 Z3 3xyz 1 2 Ex 2 5
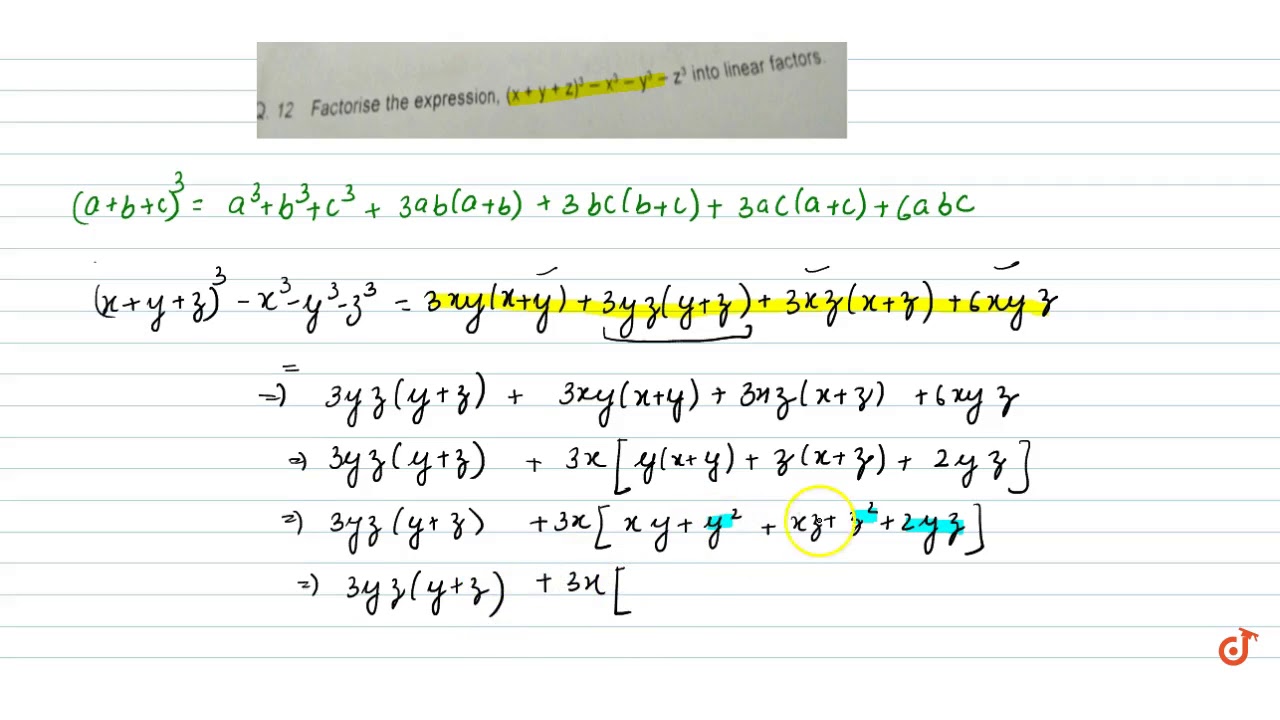



Q 12 Factorise The Expression X Y Z 3 X3 Y3 Z3 Into Linear Factors Youtube




X 3 Y 3 Z 3 Xyz Novocom Top




Factorize 27x3 Y3 Z3 9xyz Novocom Top



X Y Z 3 Expansion




Find The Value Of X 3 Y 3 Z 3 3xyz If X 2 Y 2 Z 2 And X Y Z 15 Youtube




X 3 Y 3 Z 3 Xyz Novocom Top




Is 8 X 3 Y 3 Z 3 2 Ge 9 X 2 Yz Y 2 Xz Z 2 Xy True For Nonnegative Numbers Mathematics Stack Exchange




X 3 Y 3 Z 3 3xyz X Y Z X 2 Y 2 Z 2 Xy Yz Zx A 3 B 3 C 3 3abc A B C A 2 B 2 C 2 Ab Ca Youtube




1 Using Properties Of Determinants Prove The Following X Y Z X2 Y2 Z2 X3 Y3 Z3 Maths Determinants Meritnation Com




X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X 2 X3 Y3 Z3 3xyz Mathematics Topperlearning Com T86qex55




If X 3 Y 3 Z 3 49 And X Y Z 1 Find Value Of Xy Yz Zx Xyz Please Solve The Question Math Meritnation Com
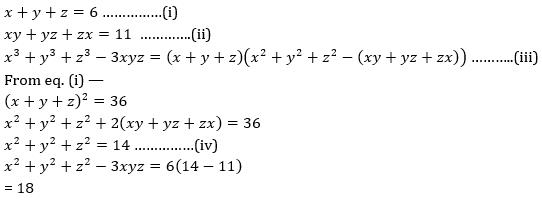



If X Y Z 6 And Xy Yz Zx 11 Then The Value Of X3 Y3 Z3 3xyz Isa 18b 36c 54d 66correct Answer Is Option A



If X Z 225 And Y 226 Then What Is The Value Of X Y Z 3xyz Quora




Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Class 9th Ex 2 5 Question 12 Youtube



Using Identities Prove That X 3 Y 3 Z 3 Or Equal To 3xyz Where X Y Z Are Positive Real Numbers Quora




X 3 Y 3 Z 3 Xyz Novocom Top




Cho X Y Z đoi Một Khac Nhau Thỏa Man X3 Y Z Z3 X Y Y3 Z X Chứng Minh Rằng X3 Y3 Z3 3xyz




If X Y Z 6 And Xy Yz Zx 12 Then Show That X3 Y3 Z3 3xyz Maths Polynomials 12 Meritnation Com




X 3 Y 3 Z 3 Xyz Novocom Top




X 3 Y 3 Z 3 Xyz Novocom Top




X 3 Y 3 3 Y 3 Z 3 3 Z 3 X 3 3 X Y 3 Y Z 3 Z X 3 Youtube




If Px Y Z X3 Y3 Z3 3 X Y Z And X B C A Y C A Gauthmath



1




With This Inequality Condition Xyz X Y Z 3 Mathematics Stack Exchange




If X Y Z 0 Show That X3 Y3 Z3 3xyz Maths Polynomials Meritnation Com




Using Factor Theorem Show That X Y Y Z And Z X Are Factors Of X Y Z 3 X3 Y3 Z3 Brainly In




If X Y Z 6 And Xy Yz Zx 11 And Xyz 6 Is Given Find The Value Of X 3 Y 3 Z 3




Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Novocom Top




18 Find The Value Of X3 Y3 Z3 Ifx Y Z 11 X2 Y2 Z2 45 And Xyz 40 Brainly In




X Y Z 2 X2 Y2 22 3 X Y Z 4 X3 Y3 Z3 Gauthmath




Example 32 Show That Determinant 2xyz X Y Z 3 Class 12




X 3 Y 3 Z 3 Xyz Novocom Top




X 3 Y 3 Z 3 Xyz Novocom Top




How To Factorise Using The Identity X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Youtube
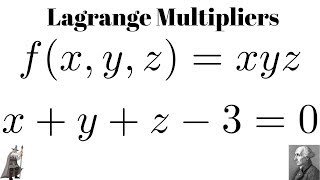



Lagrange Multipliers Maximum Of F X Y Z Xyz Subject To X Y Z 3 0 Youtube




X 3 Y 3 Z 3 Xyz Novocom Top




Let X Y Z Be Real Numbers Satisfying X Y Z 3 X 2 Y 2 Z 2 5 And X 3 Y 3 Z 3 7 Then The Value Of X 4 Y 4 Z 4 Is




X 3 Y 3 Z 3 Xyz Novocom Top




If X Y Z And X X 3 X 4 1 Y Y 3 Y 4 1 Z Z 3 Z 4 1 0 Prove That Xyz Xy Yz Zx X Y Z




Prove That X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X Novocom Top
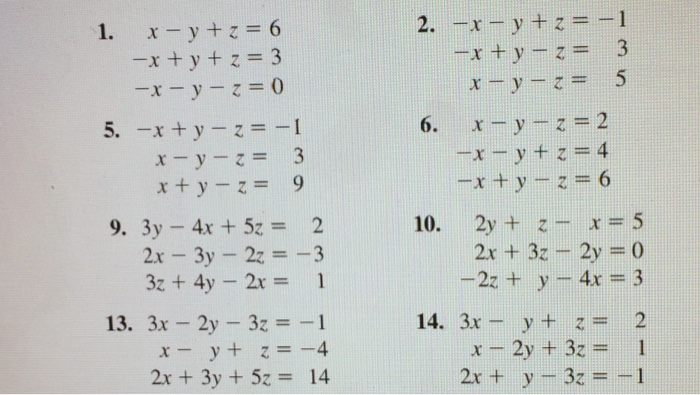



X Y Z 6 X Y Z 3 X Y Z 0 X Y Chegg Com
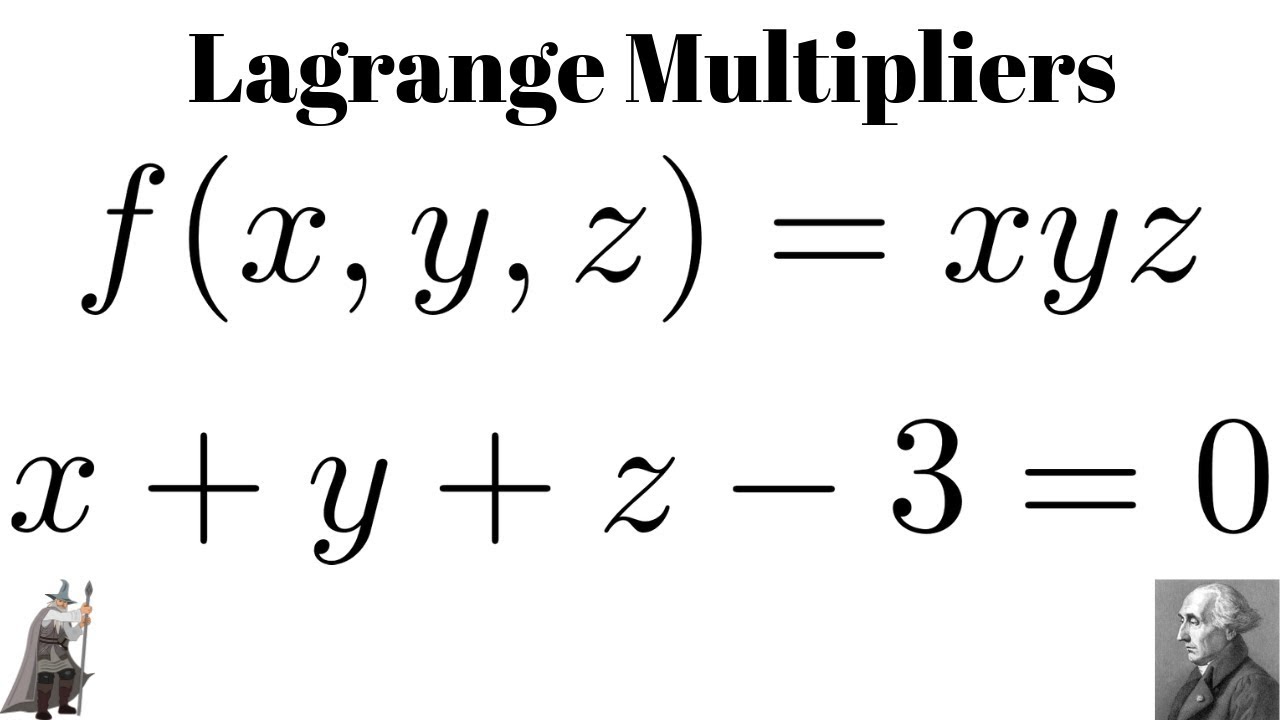



Lagrange Multipliers Maximum Of F X Y Z Xyz Subject To X Y Z 3 0 Youtube




Q32 Solve The System Of Equations X Y Z 3 X Y Z 3 Chegg Com



Razlozhit Mnogochlen Na Mnozhiteli A X Y Z 3 X 3 Y 3 Z 3b X Y Z Xy Yz Zx Xyz Shkolnye Znaniya Com




If X Y 2 2 X Y Z 4 And X2 Y Z2 3 So X3 Y Gauthmath




Factorise 27 X 3 Y 3 Z 3 9x Y Z




Prove X Y Z 3 X 2 Y 2 Z 2 9 Therefore Y X Leqq 2 Sqrt 3 Mathematics Stack Exchange




Ex 4 6 11 Solve Using Matrix Method 2x Y Z 1 X 2y Z 3 2 3y 5z 9



Y 3 Y Cheap Online



X Y Z Z X 1 2 X2 Y2 Z2 3 X Y Z 2 X Y Z 4 Gauthmath



X3 Y3 Z3 Novocom Top
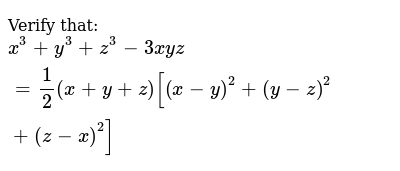



Verify That X 3 Y 3 Z 3 3xyz 1 2 X Y Z X Y 2 Y Z




If Math X Y Z 0 Math Then Math X Y Z 3 Y Z X 3 Z X Y 3 Math Quora




11 If U Ln Left X 3 Y 3




If X Y Z Xyz Show That 3x X 3 1 3x 2 3y Y 3 1 3y 2



Is The Gauss Elimination Method X 2y 3z 1 2x 3y 8z 2 X Y Z 3 Quora




If X 2 Y 2 Z 2 2 X Y Z 3 Find The Value Of 2x 3y 4z Youtube




If X Y Z 0 Then Prove That X3 Y3 Z3 3xyz Youtube




X 3 Y 3 Z 3 Xyz Novocom Top




Prove That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Brainly In




Ex 2 5 Q No 12 Verify X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube




X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Novocom Top




If Math X Y Z 0 Math What Is The Value Of Math Frac X 2 Yz Frac Y 2 Zx Frac Z 2 Xy Math Quora




Prove That 1 1 1 X Y Z X 3 Y 3 Z 3 X Y Y Z X Y Z




The Monoids Z X 3 Y 3 5 Xyz Z 3 X Y And Z X 3 Y 3 5 Download Scientific Diagram




If X Y Z 0 Then X 3 Y 3 Z 3 3 X Y Z Is Equal To A 0 B



1




X 3 Y 3 Z 3 Novocom Top




16 X Y And Z Are Real Numbers If X3 Y3 Z3 13 X Y Z 1 And Xyz 1 Then What Is The Brainly In



If X Y Z 10 Xy Yz Zx 15 And Xyz 12 Then Find The Values Of I X 3 Y 3 Z 3 And Ii X 2 Y 2 Z 2 Sarthaks Econnect Largest Online Education Community




Phan Tich đa Thức Thanh Nhan Tử X Y Z 3 X 3 Y 3 Z 3 Toan Học Lớp 8 Bai Tập Toan Học Lớp 8 Giải




Graphing Software Fails To Include Point 1 1 1 In The Graph Of X 3 Y 3 Z 3 3xyz 0 Why Mathematics Stack Exchange



0 件のコメント:
コメントを投稿